Daily Summary(1)

2.28_Math

1. 排列：由1，2，3，….n组成的一个有序数值叫做n级排列，中间不能缺数
2. 逆序数：逆序的总数
   N（54123）=4+3=7
3. 数逆序数
   • 从第一个开始，数后面比它小的
   • 切记顺序不能乱来
4. 逆序数为奇数，奇排列
   逆序数为偶数，偶排列
5. 对换
   • 54123进行1次对换，例如54213，由奇排列变为偶排列
   • 进行奇数次对换，奇排列变偶排列，偶排列变奇排列
   • 进行偶数次对换，奇偶不变
6. 定理：n级排列中，奇排列，偶排列各占一半
7. 标准排列：1，2，3，…..，n
8. N（123….n）=0

3.1_Math

1、n阶行列式：（三种定义）
第一种定义：行标取标准排列，列标取排列的所有可能，从不同行不同列取出n个元素相 乘，符号由列标排列的奇偶性决定的，一共由n!项。
第二种定义：列标取标准排列，行标取排列的所有可能，从不同行不同列取出n个元素相 乘，符号由行标排列的奇偶性决定的，一共由n!项。

2、下三角行列式 上三角行列式

3、对角形行列式

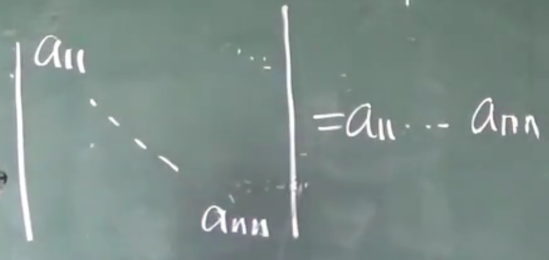
4、山寨系列

• 5、纯数字的行列式解法：转换为上三角行列式（主对角线元素相乘）
  • 所用性质：用行列式的一行加上去另一行的倍数，行列式不变。
  • 步骤：
    1. 先处理第一列，再处理第二列，再处理第三列
    2. 第一列处理完，第一列不在参与运算
  • 尽量别用“第X行去减第X行”的说法（防止自己糊涂）
  • 建议使用：
    1. 第X行乘X，加到第X行上去
    2. 第X行加到第X行上去
    3. 第X行乘（-X），加到第X行上去
• 6、按行（列）展开：用某一行的每个元素乘对应的代数余子式，等于原行列式的值
  • 用途：对行列式降一阶
  • 技巧：选择0较多的一行（列）去展开
• 7、异乘变零定理：某一行元素与另一行元素的代数余子式相乘，乘积之和为0

3.2_Math

1. 负向量：与原向量长度相等，方向相反
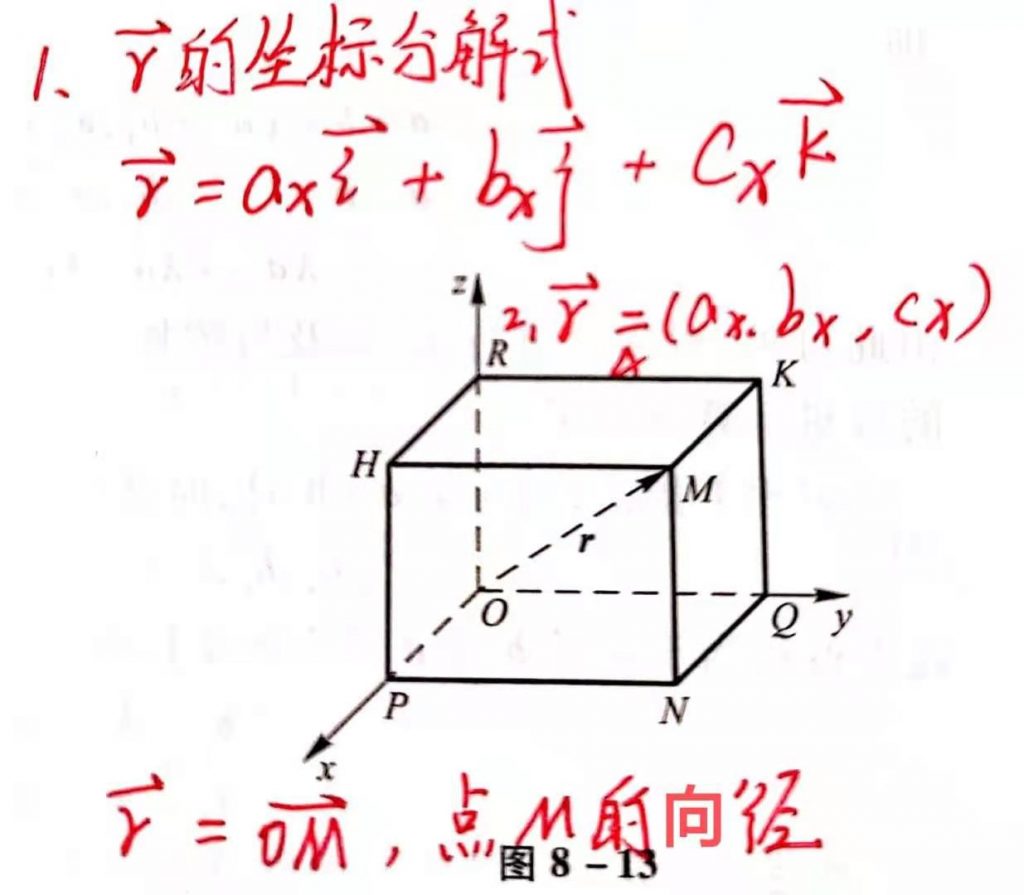
2. 方向角：非零向量r与三条坐标轴的夹角α、β、γ
3. 方向余弦：cos α,cos β,cos γ
   • cos²α +cos²β+cos²γ= 1
4. 向径的定义：