Daily Summary(60)

5.10_Math

1、二次型→矩阵表达式

①平方项的系数直接做成主对角线
②交叉项的系数除以2放到两个对称的相应位置上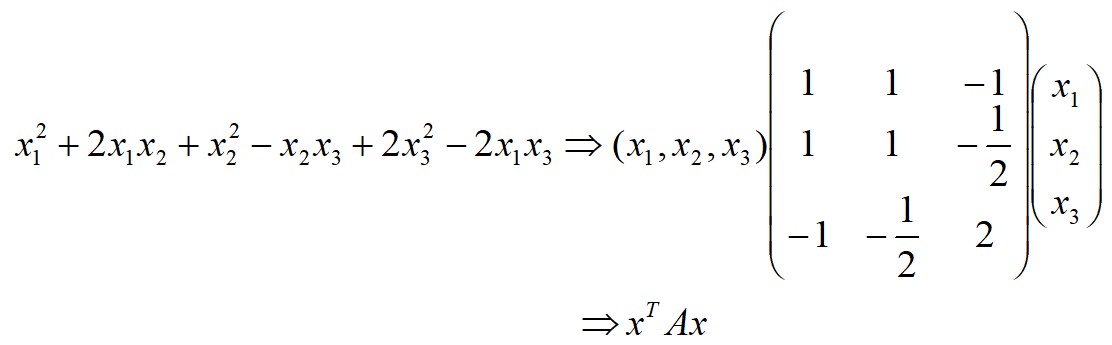

A：二次型的矩阵，对称矩阵，A^T=A

2、矩阵表达式→二次型（检查矩阵是否对称）

①主对角线元素直接做成平方项的系数
②取主对角线右（左）上角元素乘以2做为交叉项的系数

3、标准型

• 定义：d₁y₁²+d₂y₂²+···+d_ny_n²(只有平方项)
• 线性替换：存在X=CY，使得f(X)=X^TAX=(CY)^TACY=Y^T(C^TAC)Y，C^TAC为对角型
  • |C|≠０，称为可逆，非退化替换；|C|＝０，称为退化替换

４、合同

• 定义：A，B为ｎ阶方阵，存在可逆矩阵C，使得C^TAC＝B，称A，B合同
• 性质：
  1. 反身性：A≅A
  2. 对称性：A≅B→B≅A
  3. 传递性：A≅B，B≅C→A≅C
  4. A≅B，r(A)=r(B)
  5. A≅B，A^T=A⇔B^T=B
  6. A≅B，A，B可逆，A^-1≅B^-1
  7. A≅B，A^T≅B^T
• 充要条件：有相同的秩，有相同的正惯性指数（负惯性指数）

５、概念间联系