10.5_Data structure
特殊矩阵的压缩存储
1、对称矩阵
特点:aij=aji(i,j=0,1,2,···,n-1)
方法:每一对对称元素,只分配一个元素的存储空间,从而将n2个元素压缩到n(n+1)/2个元素空间
公式:按行为主,顺序存储,存放对称矩阵的下三角中的元素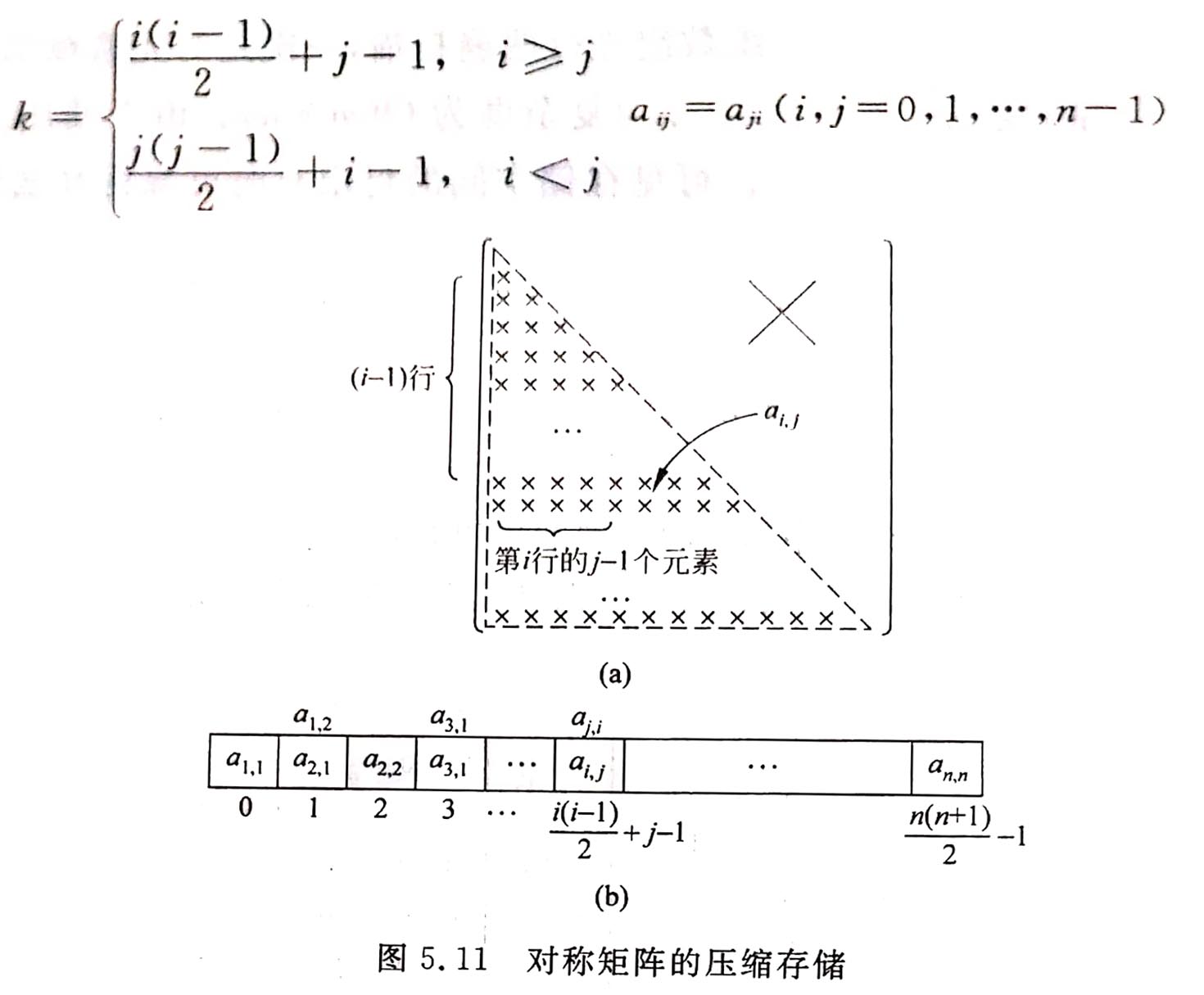
2、带状矩阵
特点:所有非零元素都集中在以主对角线为核心的带状区域中,以三对角矩阵较为常见
方法:只存放非零元素,以及矩阵的维度
公式: 按行为主,顺序存储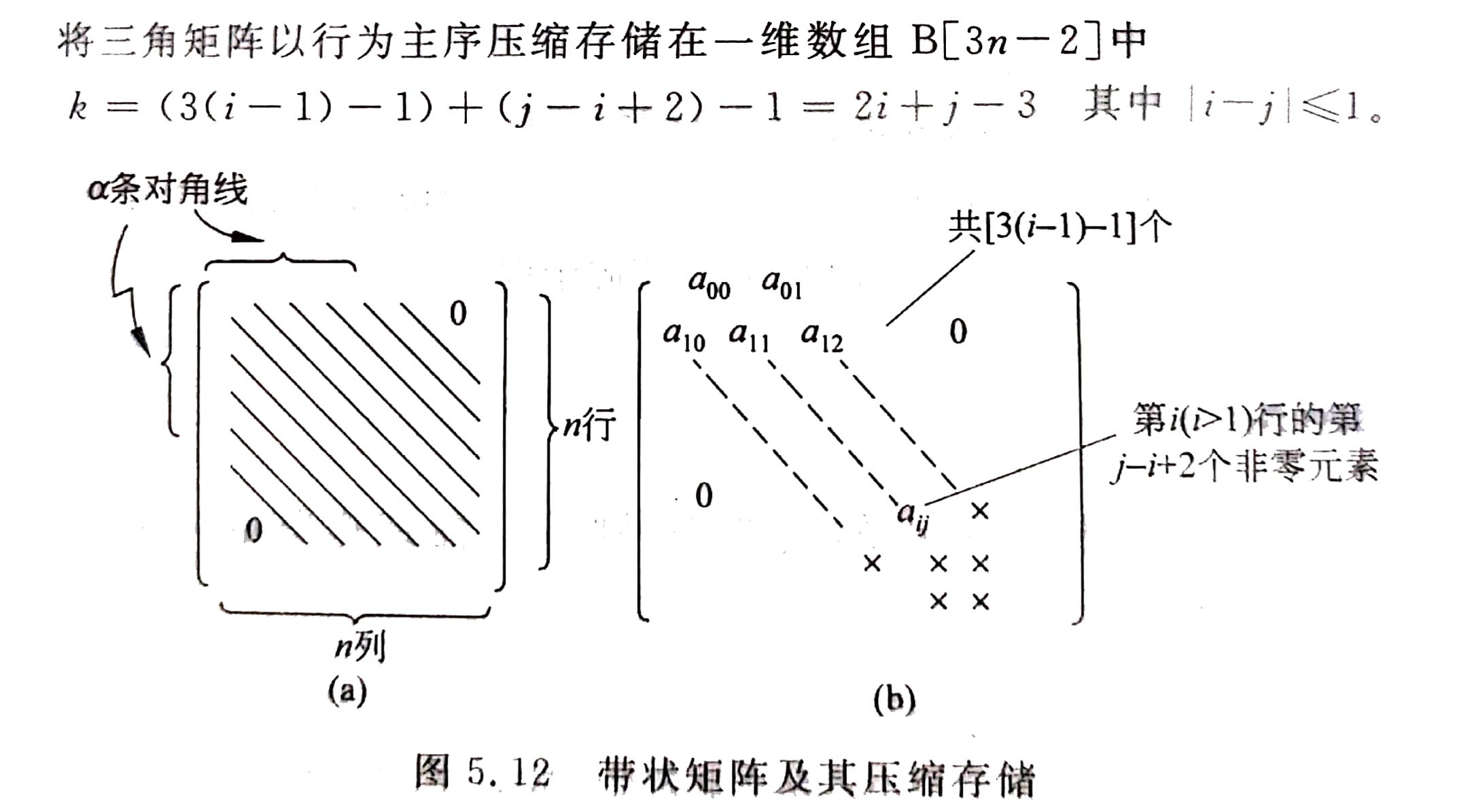
随机稀疏矩阵的压缩存储
稀疏矩阵的表示方法是否有效要看它是否便于稀疏矩阵的运算,下面以矩阵的转置运算为例进行讨论
1、按需点菜
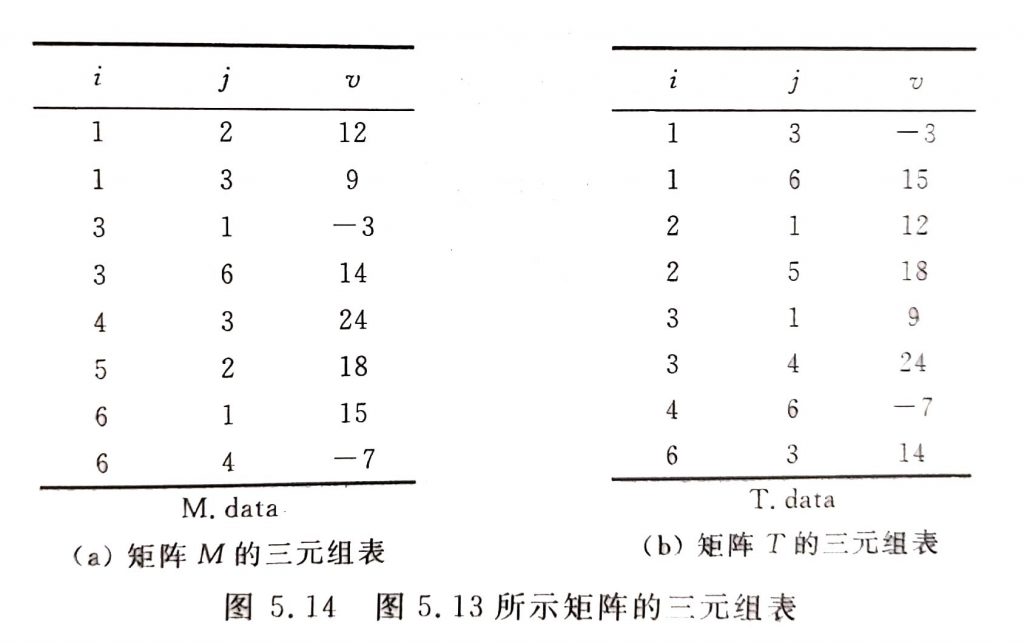
一种方法是“按需点菜”。由于T.data[]中的元素是以矩阵T的行序为主序的顺序排列的。换句话说,是以矩阵M的列序为主序的顺序排列的,则可以按M的列号顺序依次从M.data[]中“找出”元素进行“行列转换”之后插入T.data[]中。例如对图5.14(a)所示矩阵的非零元素,先依次转换(3,1,-3)和(6,1,15),再依次转换(1,2,12)和(5,2,18),依次类推。由于对M的每一列都要对M的三元组扫描一遍,因此如此处理的算法的时间复杂度为O(nXt),其中n为矩阵M的列数,t为M中的非零元的数目。
2、按位就坐
另一种处理方法是“按位就座”。只对M.data[]进行一次扫描,就使所有非零元的三元组在T中“一次到位”。为实现之,首先应分析每个非零元在T.data[]中的位置的规律。如非零元(1,2,12)经转换后变成(2,1,12),应直接安置在T.data[]中第三个非零元的位置,因为对矩阵T而言,第一行中只有两个非零元,而(2,1,12)是第二行中第一个非零元。由此,如果能预先计算出T矩阵中每一行的第一个非零元所应该在的位置,就可以实现非零元在T.data[]中的一次到位。为此,只要先计算出矩阵T中每一行的非零元的数目(即原矩阵M中每一列的非零元数目),就可以通过累计进而求得转置矩阵T中每一行的非零元在T.data[]中的起始位置。

No responses yet