Daily Summary(28)

4.2_Math

线性相关与线性无关定理

• 定理1：向量组α₁，α₂，···，α_s（s≥2）线性相关，则向量组中至少有一个向量可由其余s-1个向量线性表示
  
  
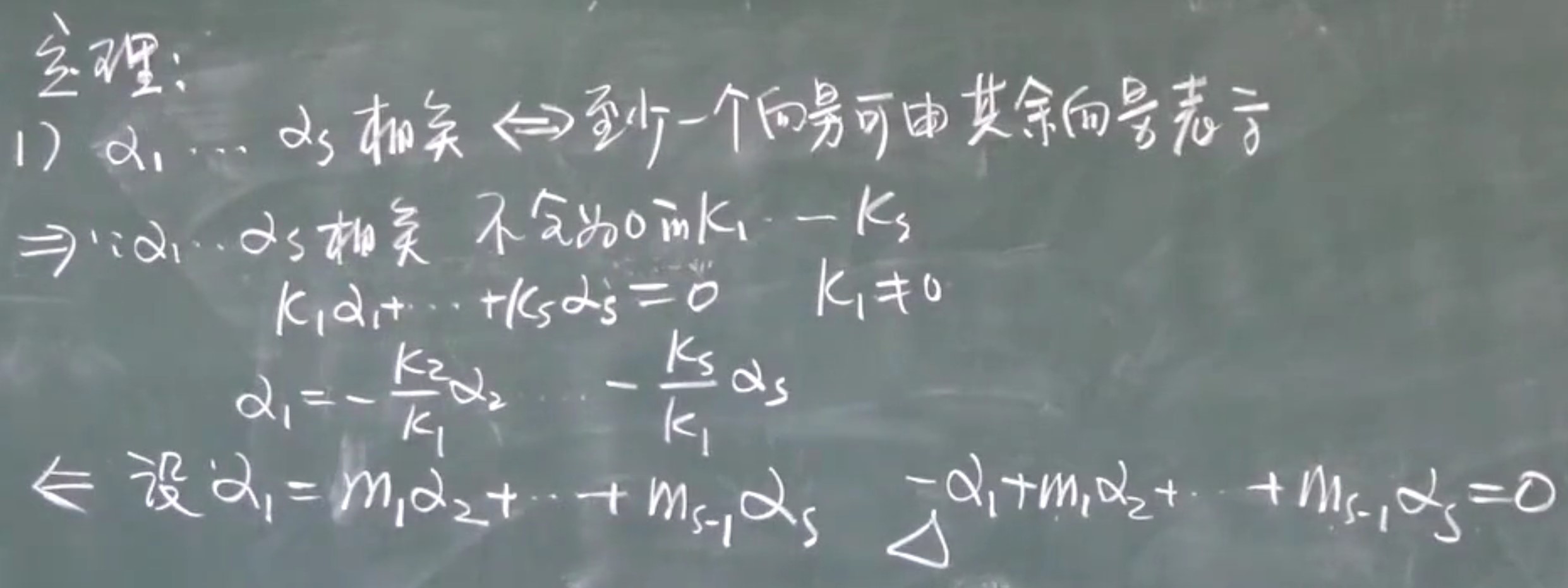
• 定理2：设向量组α₁，α₂，···，α_r线性无关，而向量组α₁，α₂，···，α_r，β线性相关，则β能由α₁，α₂，···，α_r线性表示，且表示式是唯一的
  (线性表示)
  (唯一的)
  
• 定理3：当m＞n时，任意m个n维向量线性相关
  
  
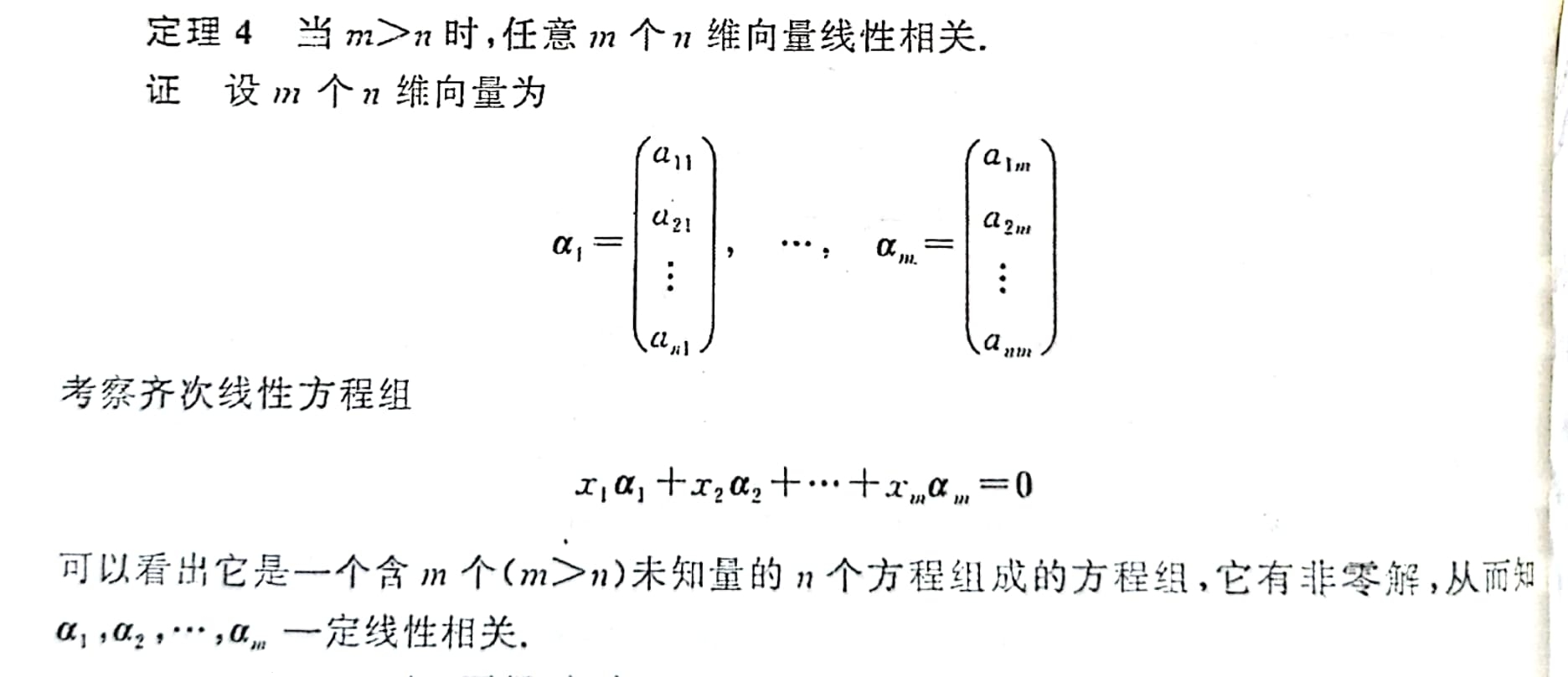
• ***定理4（替换定理）：设α₁，α₂，···，α_r与β₁，β₂，···，β_s是两个向量组，如果①向量组α₁，α₂，···，α_r可以经β₁，β₂，···，β_s线性表出；②r＞s，那么向量组α₁，α₂，···，α_r线性相关
  推论：如果向量组α₁，α₂，···，α_r可以经向量组β₁，β₂，···，β_s线性表出，且α₁，α₂，···，α_r线性无关，那么r≤s