Daily Summary(34)

4.9_Math

1、k阶子式

定义：对任意一个矩阵，任取k行，任取k列的一个行列式

2、矩阵的秩

• 定义：非零子式的最高阶数
• 记作：r(A)=a（eg.r(A)=5，A为矩阵）
• 类型：A_m×n，0≤r(A)≤min{m，n}
  • 满秩：r(A)=min{m，n}
    • r(A)=m，取所有行，记作：行满秩
    • r(A)=n，取所有列，记作：列满秩
  • 降秩：r(A)<min{m，n}
• 性质：
  • r(0)=0
  • A为方阵，A满秩⇔A可逆
  • 初等（行列）变换不改变矩阵的秩
  • r(A)=r(A^T)
  • 矩阵乘可逆矩阵，矩阵的秩不变
    A_m×n，P为m阶可逆方阵，Q为n阶可逆方阵
    r(A)=r(PA)=r(AQ)=r(PAQ)
• 定理：r(A)=r⇔有一个r阶子式不为0，所有r+1阶子式为0

3、阶梯形矩阵

• 定义：
  • 若有零行，零行在非零行下边
  • 左起首非零元左边零的个数随行数增加而严格增加
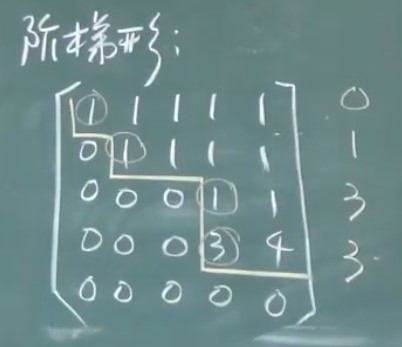    (不是阶梯形)
  • 划线法：横线可跨多个数，竖线只跨一个数
• 行简化阶梯型：
  • 非零行的首非零元是“1”
  • 首非零元所在列的其余元素都是“0”
  • 矩阵的秩=非零行的行数

4、求矩阵的秩

通过初等行（列）变换→阶梯形，非零行的行数是矩阵的秩