Daily Summary(96)

9.18_Physical

1、驻波

条件：两列相干波①振幅相同②相向传播发生干涉

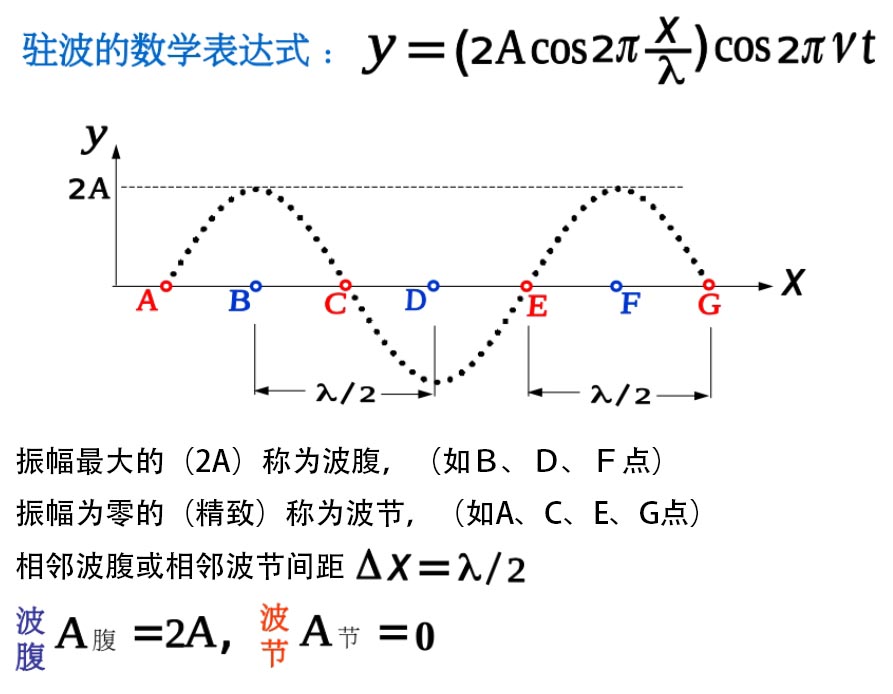
2、半波损失

波从波疏介质传播到波密介质的界面时，反射波会发生π的相位突变，相当于波长损失了λ/2，界面处的合成振动总是形成波节
波从波密介质传播到波疏介质的界面时，反射波不会发生π的相位突变，界面处的合成振动总是形成波腹部

3、多普勒效应

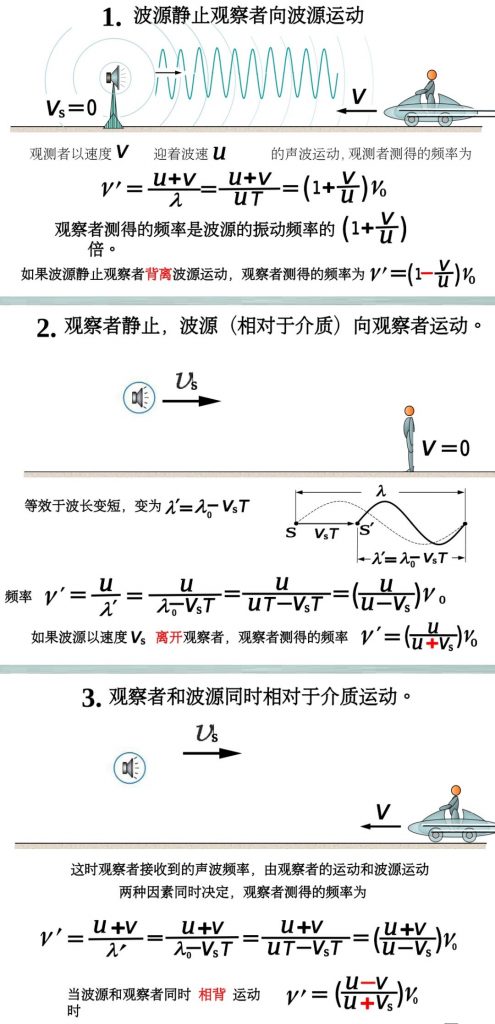
例题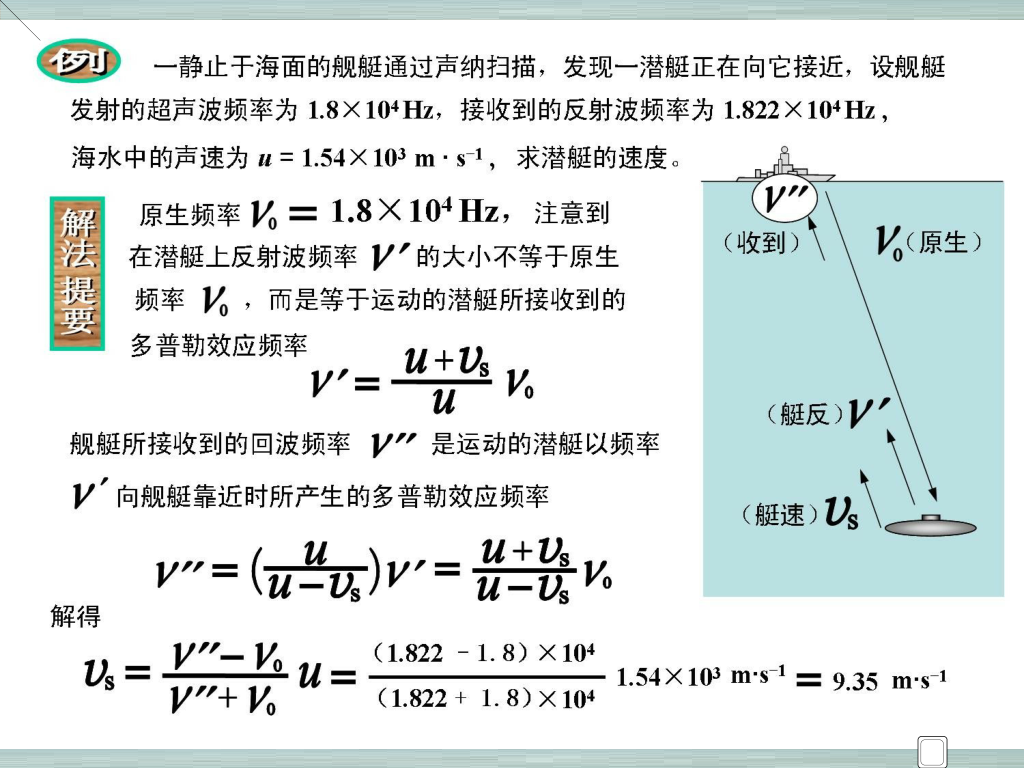

9.18_Discrete

1、一阶逻辑各种概念

• 个体常项：表示具体的或特定的个体的词，一般用小写的英文字母a,b,c,…表示
• 个体变项：表示抽象的,或泛指的个体的词，常用小写英文字母x,y,z,…表示
• 个体域(或论域)：个体变项的取值范围。
  个体域可以是有限的集合，例如,{1,2,3,4}、{a,b,c}、{计算机,2,狮子}，
  也可以是无限的集合，例如，自然数集合、实数集合等
• 全总个体域：当无特殊声明时，个体域由宇宙间的一切事物组成
• 谓词常项：表示具体性质或关系的谓词，用大写英文字母F,G,H,…表示，例如,用F表示“……是无理数”
• 谓词变项：抽象的或泛指的谓词，也用F,G,H…表示
• 元数：谓词中包含的个体词数.
• n元谓词：含n(n≥1)个个体词的谓词.
  ※一元谓词是表示个体词性质的。当n≥2时,n元谓词表示个体词之间的关系
• 0元谓词：不带个体变项的谓词。
  0元谓词常项都是命题。简单命题都可以用0元谓词常项表示，因而可将命题看成谓词的特殊情况
• 量词：全称量词(∀)、存在量词(∃)
• 特性谓词：例如，谓词M(x)：x是人.
  
  在使用量词时,应注意以下6点
• (1)在不同的个体域中,命题符号化的形式可能不一样
• (2)如果事先没有给出个体域,都应以全总个体域为个体域
• (3)在引入特性谓词后,使用全称量词与存在量词符号化的形式是不同的,请注意上面()、(*)两种形式
• (4)个体域和谓词的含义确定之后,n元谓词要转化为命题至少需要n个量词
• (5)当个体域为有限集时,如D={a1,a2,…,an},由量词的意义可以看出,对于任意的谓词A(x),都有
  ①∀xA(x)⇔A(a₁)∧A(a₂)∧…∧A(a_n)
  ②∃xA(x)⇔A(a₁)∨A(a₂)∨…∨A(a_n)
  这实际上是将一阶逻辑中命题公式转化为命题逻辑中的命题公式了
• (6)多个量词同时出现时,不能随意颠倒它们的顺序.颠倒后可能与原来的含义完全不同

2、定义1-7