3.19_Physical
1、基本概念
- 角位移(dθ):dθ=θ2-θ1逆时针旋转时dθ为正
- 角速度(ω):ω=dθ/dt,注意:ω的正负与dθ的正负有关
- 角加速度(α”Alpha”):α=dω/dθ,注意:α的正负与dω的正负有关,α与ω同号加速,异号减速
- 角动量(L):L=r×p=r×mv其中r是质点相对O点的位矢(位置矢量)(冲量P=mv)
- 力矩(M):M=r×F该点到力的作用线所引垂线的长度(即力臂)乘以力的大小(力F)
- 力矩M等于角动量L对时间t的变化率M=dL/dt
- 冲量矩(H):H=Mt=r×F×t量度力矩对转动物体的时间累计效应的物理量(冲量I=Ft)
注意:上述变量的方向;若为叉乘,方向遵循右手螺旋定则 - 有心力:方向恒指向或背向一固定中心的力
- 有心力的力矩M=r×f=0
- 质点角动量守恒定理:当质点所受到的外力矩为零时,其角动量守恒
- 刚体的转动惯量(I/J):组成刚体的各质元质量与质元到转轴距离平方乘积的代数和
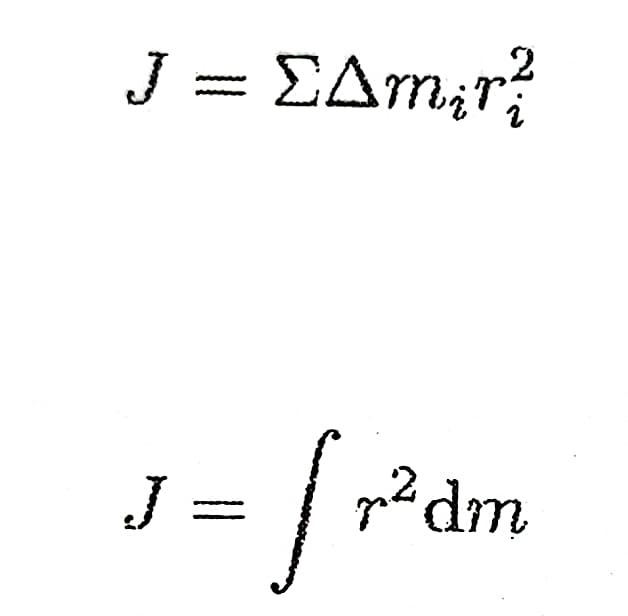
- 刚体对定轴角动量:
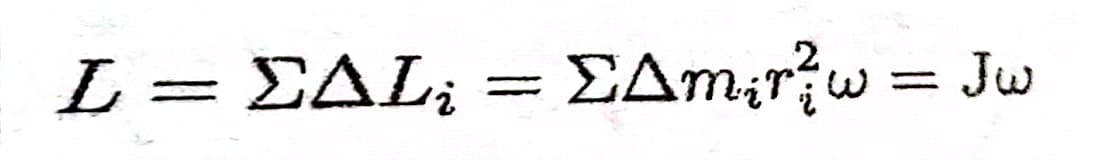
2、公式(标量式)
- 弧长(ds):ds=rdθ
- 线速度(v):v=ds/dt=rω
- 切向加速度(at):at=dv/dt=rα(Alpha)
- 法线加速度(an):an=v2/r=rω2
- 总加速度(a):a2=at2+an2
- ω=ω0+αt
- θ=θ0+ω0t+1/2αt2
- ω2-ω02=2α(θ-θ0)
- L=Jω
- Mt=Jω→M=Jα
3、求转动惯量
一般方法
特殊值

4、角动量守恒条件:合外力矩等于0(满足以下其一)
- 力平行于转轴
- 力与转轴相交(或力为有心力)
- 内力远大于外力
5、角动量守恒表现:角动量为常数(Iω=C)
- I不变,ω也不变
- I改变,ω也改变(一增一减)
6、题型
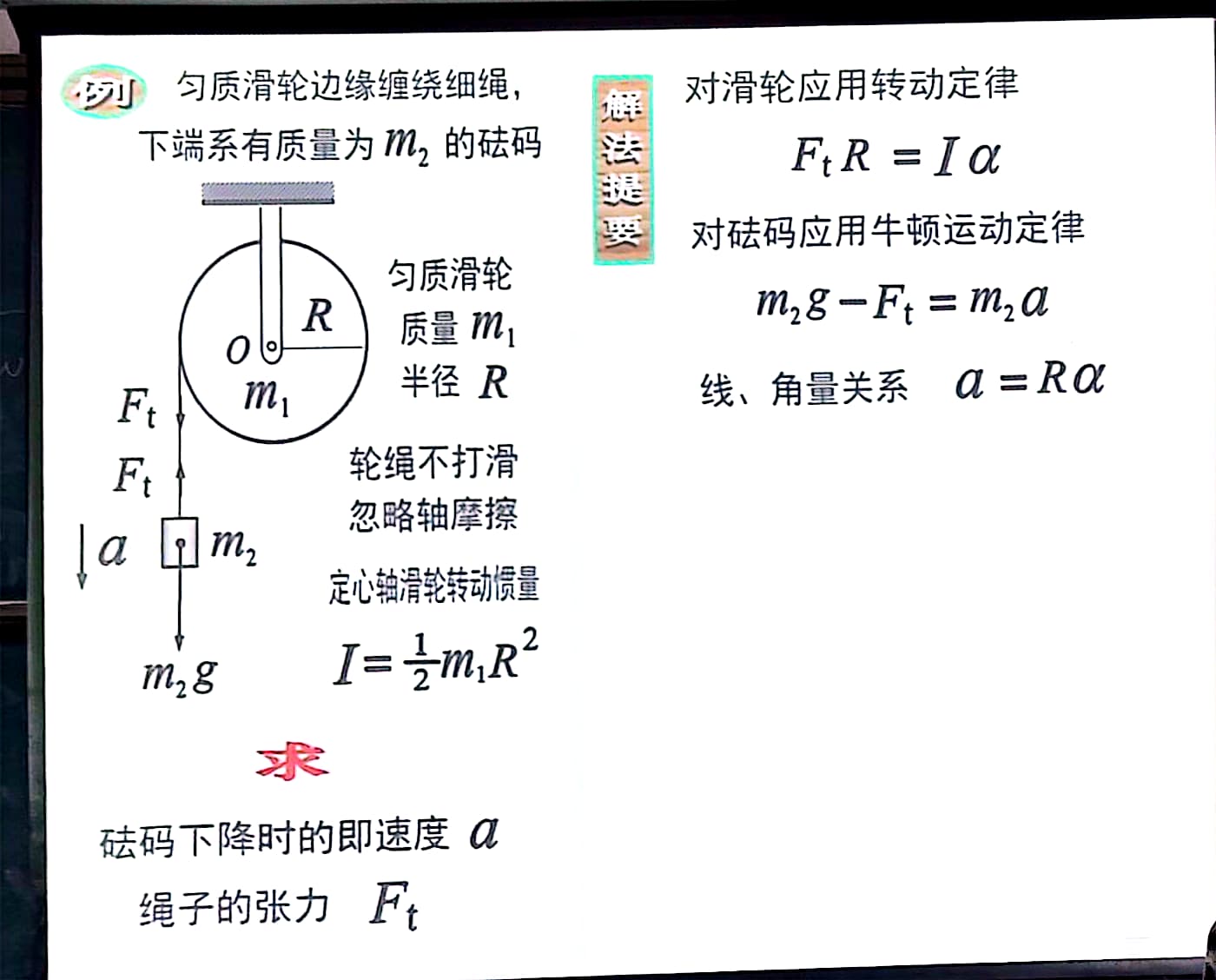
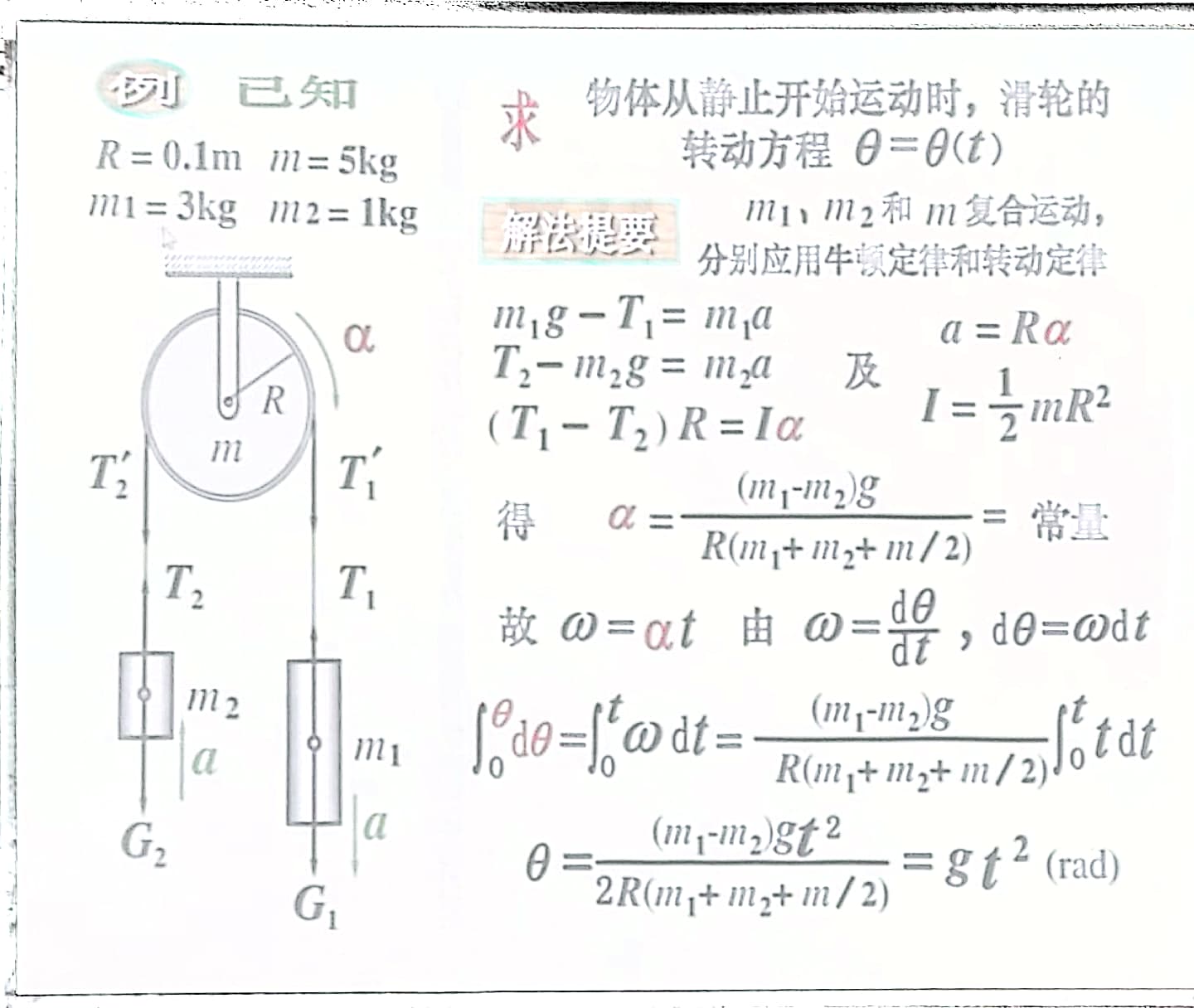

No responses yet