3.22_Math
1、矩阵等价
- 定义:A经过初等变换得到B,A≌B
- 性质:
- 反身性:A≌A
- 对称性:A≌B→B≌A
- 传递性:A≌B,B≌C→A≌C
2、定理1
任意矩阵可通过初等变换化为标准形,即A≌标准形
3、初等变换
变换形式:
1)交换两行(列)
2)用k(k≠0)乘某一行(列)
3)某一行的L倍加到另一行(列)上去
注意:矩阵变换时,两矩阵用→相连,不可以用=
4、方阵初等变化后行列式值的改变
| 初等变换形式 | 变换后行列式的值 |
| 交换两行(列) | |A|=-|B| |
| 用k(k≠0)乘某一行(列) | k|A|=|B| |
| 某一行的L倍加到另一行(列)上去 | |A|=|B| |
5、初等矩阵
- 定义:对E做一次初等变换得到的矩阵
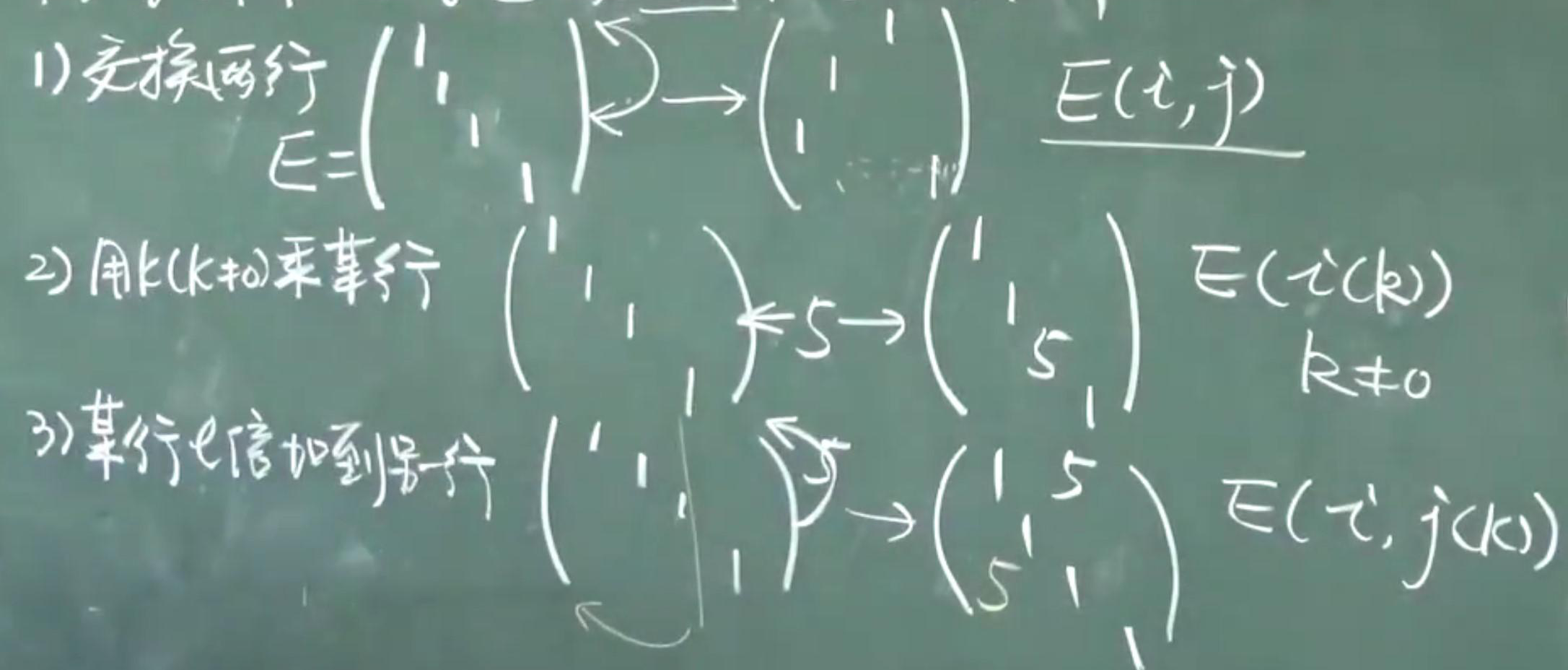
- 性质:
- A是任意矩阵,用某种初等方阵左乘A,相当于对A实施同种初等行变换(左↔行)
- A是任意矩阵,用某种初等方阵右乘A,相当于对A实施同种初等列变换(右↔列)
- 用途:用初等变换进行的操作,可以转化为左乘或右乘相应的初等方阵
6、初等矩阵的逆矩阵和转置
- 初等方阵的行列式的值
- |E(i,j)|=-1
- |E(i(k))|=k(k≠0)
- |E(i,j(k))|=1
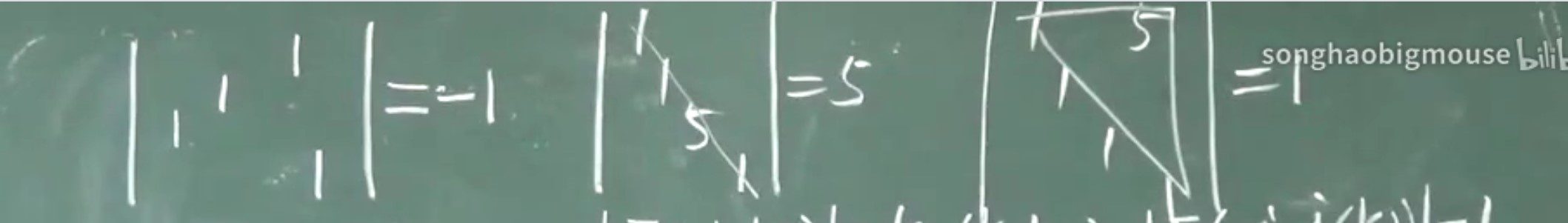
- 性质
- 初等方阵均可逆,其逆矩阵也是初等方阵
- E-1(i,j)=E(i,j)
- E-1(i(k))=E(i(1/k))
- E-1(i,j(k))=E(i,j(-k))
- 初等方阵的转置也是初等方阵
- 初等方阵均可逆,其逆矩阵也是初等方阵
7、定理2
任意矩阵A,存在初等方阵P1,P2…Ps,Q1,Q2…Qt,可以使Ps···P1·A·Q1···Qt为标准形
推论:A≌B↔存在可逆P,Q,使PAQ=B

No responses yet