5.2_Math
1、相似矩阵
- 概念:A,B为n阶方阵,存在n阶可逆矩阵P,使P-1AP=B,则称A~B
- 特性:
- 反身性:A~A,E-1AE=B
- 对称性:A~B→B~A
- 传递性:A~B,B~C=A~C
- 性质:
- A~B,则A,B有相同的特征值,|A|=|B|,tr(A)=tr(B)***
- A~B,则A可逆⇔B可逆,A-1~B-1
- A~B,则Am~Bm
- A~B,则r(A)=r(B)
2、矩阵与对角形相似的条件(P-1AP=Λ)
定理1:A~Λ ⇔ A有n个线性无关的特征向量
推论:若A有n个互异的特征值,则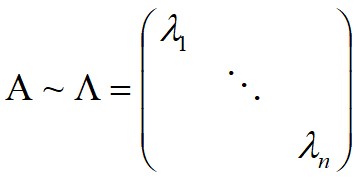
定理2:A~Λ ⇔ 对每个ri特征根,其基础解系有ri个解,n-r(λiE-A)=ri
eg.五阶方阵A~Λ,有三重根λ1=λ2=λ3=2,(λiE-A)x=0的基础解系也是三
3、题型
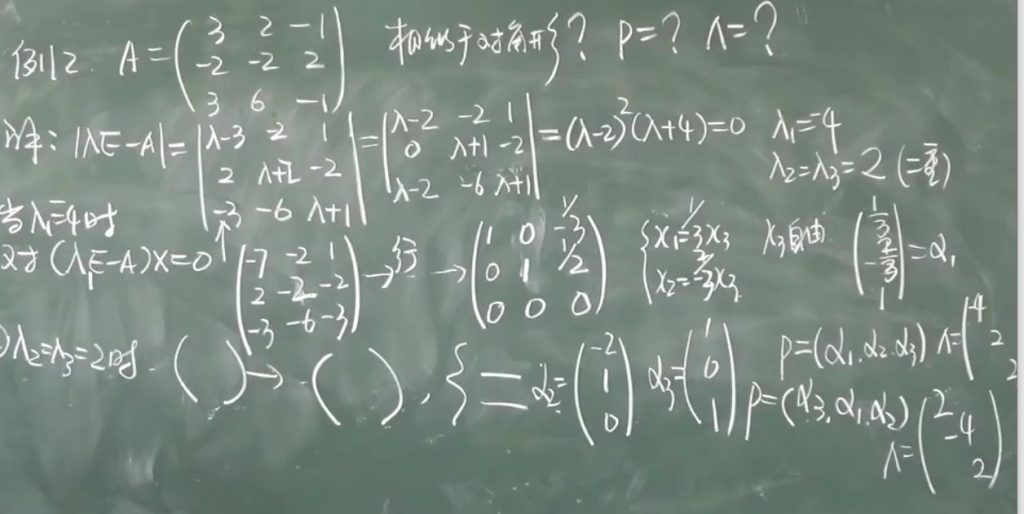
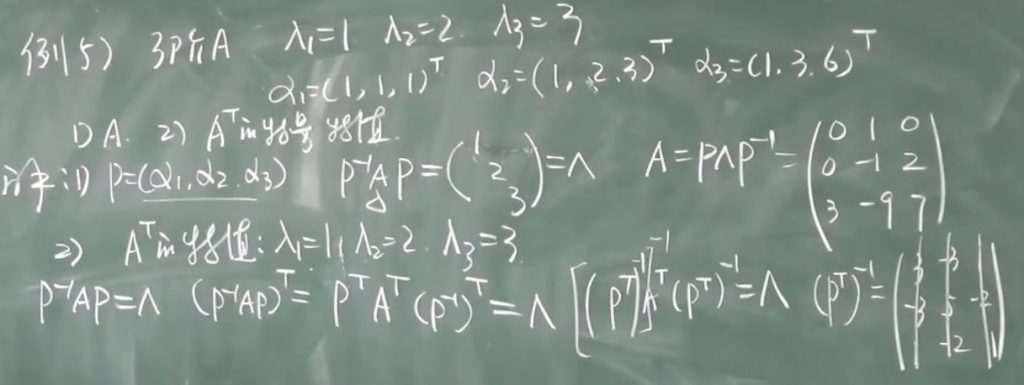
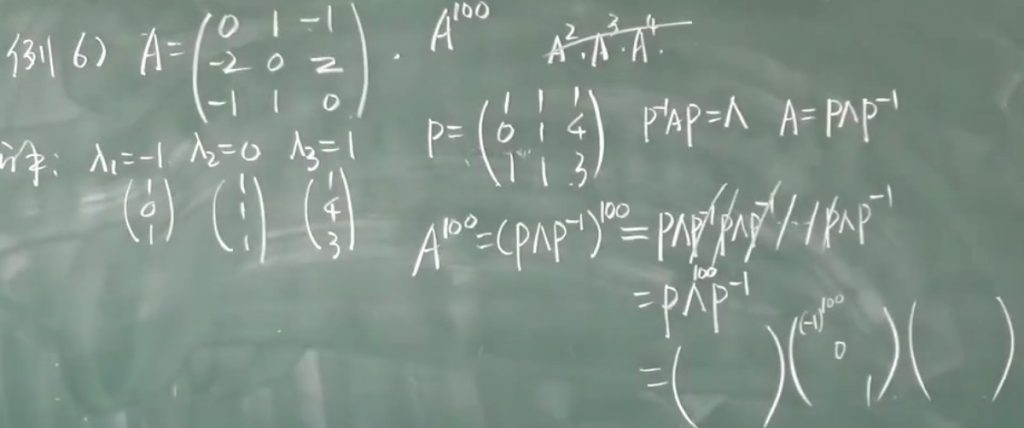

No responses yet