Daily Summary(54)

5.3_Math

1、内积（α，β）

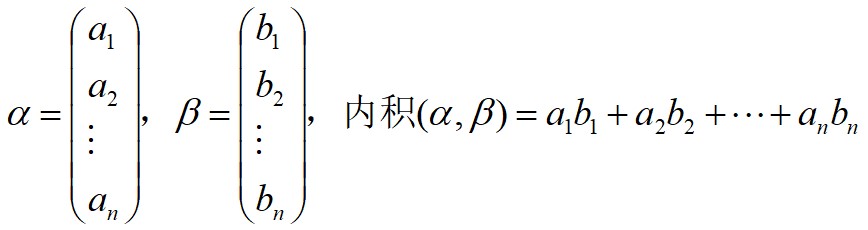
内积是个数字

*最后一定是行向量乘列向量

• 性质：
• (α，α)≥0，(α，α)=0⇔α=0
• (α，β)=(β，α)
• (kα，β)=k(α，β)
• (α+β，γ)=(α，γ)+(β，γ)

2、向量的长度（范数，模）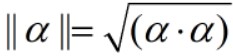

性质
柯西施瓦茨不等式：
三角不等式：

3、正交

• 定义：(α，β)=0，即α⊥β
  • (α，α)=0⇔α=0
  • 零向量与任意向量都正交
• 正交向量组：α₁，α₂，···，α_s两两正交（不含有零向量）
  • 性质：(α_i，α_j)=0
  • 标准正交向量组：每个向量都是单位向量
    • 性质：(α_i，α_i)=1，(α_i，α_j)=0
• 定理：α₁，α₂，···，α_s是正交向量组，α₁，α₂，···，α_s线性无关