Daily Summary(55)

5.4_Math

1、施密特正交化

给一组无关的α₁，α₂，···，α_r，求与之等价的正交的β₁，β₂，···，β_r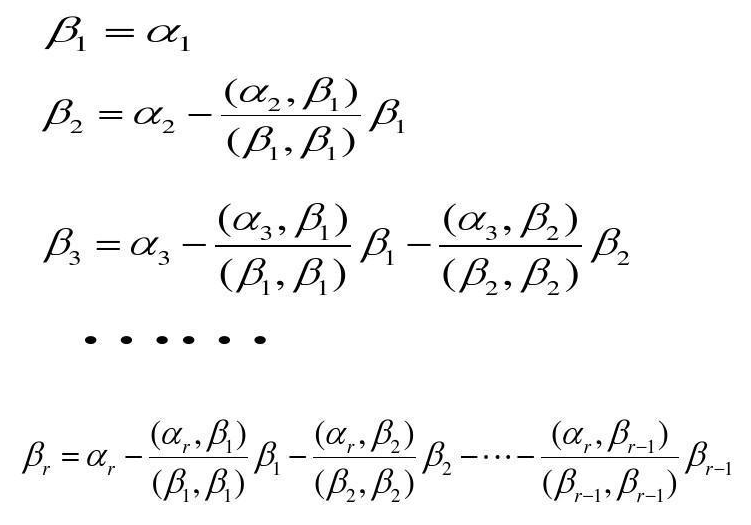

2、正交矩阵

• 定义：A为n阶方阵，A^TA=E
• 性质：
  1. |A|=1或者|A|=-1
  2. A^-1=A^T，且A^-1与A^T均正交
  3. A，B均正交，AB也正交
  4. α，β为n维列向量，（Aα，Aβ）=（α，β）
• 定理：A正交⇔A的列（行）向量组是标准正交向量组

3、实对称矩阵的对角化

• 基础概念
  • 实对称矩阵：A^T=A（一定能对角化）
  • 定理：实对称矩阵A的不同特征值的特征向量正交
  • 正交相似：A，B同阶，存在正交矩阵P，使得P^-1AP=B
• 给实对称A，求正交Q，Λ，使得Q^-1AQ=Λ
  步骤
  1. 求特征值，特征向量
  2. 特征向量正交化，单位化
  3. 做成列，构成Q
  4. 求Λ
• 
  多种情况（一般为3阶实对称矩阵）
  1. 三个特征根都是单根，特征向量已经正交化，直接单位化
  2. 一个单根，一个二重根，因为单根对应特征向量与二重根对应的正交，所以只需做二重根对应特征向量的施密特正交化，再做单位化
  3. 一个三重根，对一个三重根对应的三个特征向量做施密特正交化，再做单位化