3.5_Math
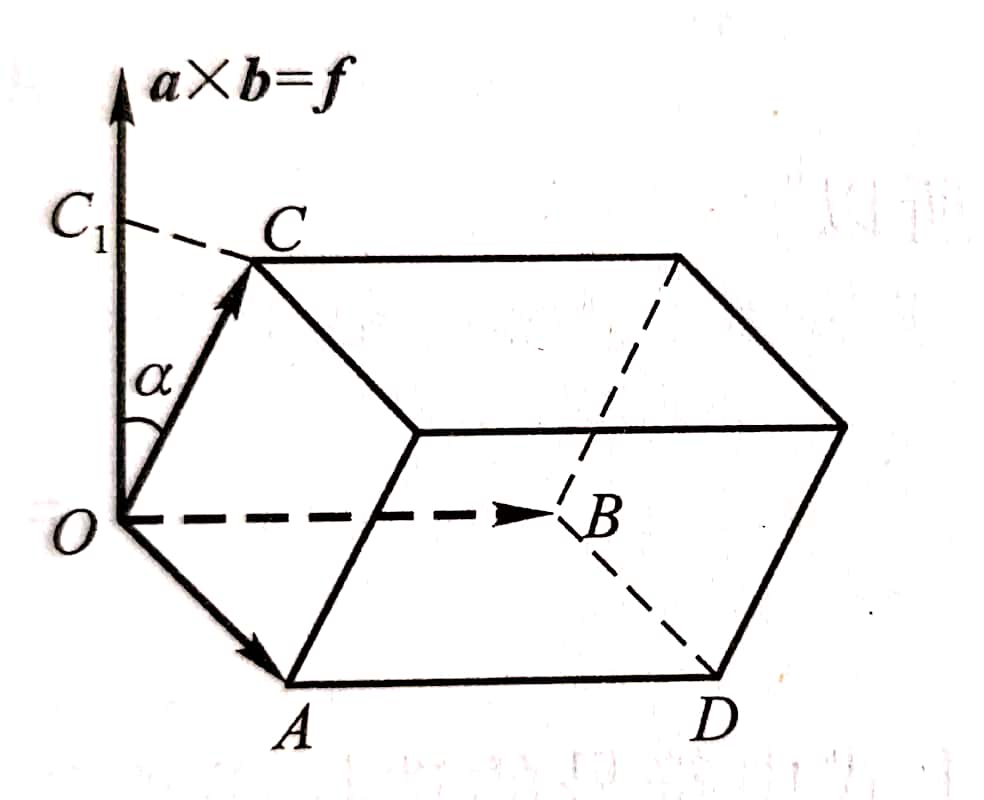
1、混合积:(a×b)⋅c , 记作[abc]
向量的混合积是一个数,他的绝对值表示以向量a、b、c为棱的平行六面体的体积
2、平面的一般方程
方程形式:Ax+By+Cz+D=0
其中垂直于目标平面的法向量为n=(A,B,C)
(1)当D=0时,方程成为Ax+By+Cz=0,表示一个通过原点的平面
(2)当A=0时,方程成为By+Cz+D=0,法线向量n=(0,B,C)垂直于x轴,表示一个平行于(或包含)x轴的平面
同理,当B=0和C=0时,表示一个平行于(或包含)y轴和z轴的平面
(3)当A=B=0时,方程成为Cz+D=0,法线向量n=(0,0,C)同时垂直于x轴和y轴,表示一个平行于(或重合于)xOy面的平面
同理,当B=C=0和A=C=0时,表示一个平行于(或重合于)yOz面和xOz面的平面
3、平面的点法式方程
建立条件:空间内任意一点、与目标平面垂直的法向量
方程形式:A(x-x0)+B(y-y0)+C(z-z0)=0
其中空间内定点为M(x0,y0,z0),垂直于目标平面的法向量为n=(A,B,C)
4、平面的三点式方程
建立条件:已知空间内不共线的三个点M1,M2,M3
运用方法:
a.设平面方程为A(x-x0)+B(y-y0)+C(z-z0)=D的形式,并将三点分别带入
b.联立三个方程,其中A,B,C为所求未知数
c.通过三阶行列式进行求解
已知三点没M1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3)
n⊥M1M2,n⊥M1M3⟹n=M1M2×M1M3
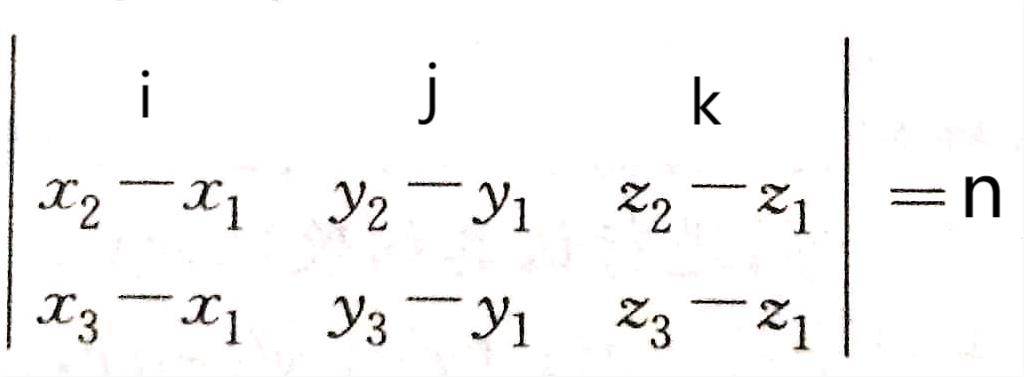
5、平面的截距式方程
建立条件:已知三点坐标分别在三个坐标轴上
方程形式: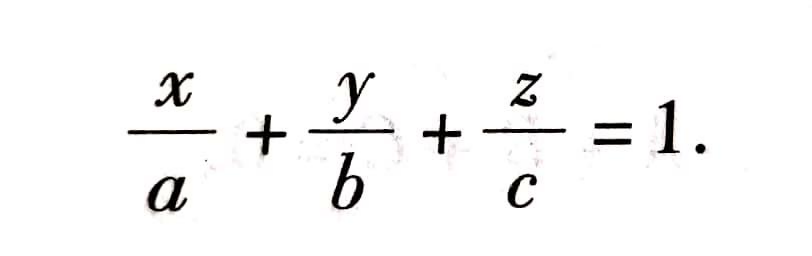
其中,a,b,c依次叫做平面在x、y、z轴上的截距
6、点到平面的距离公式
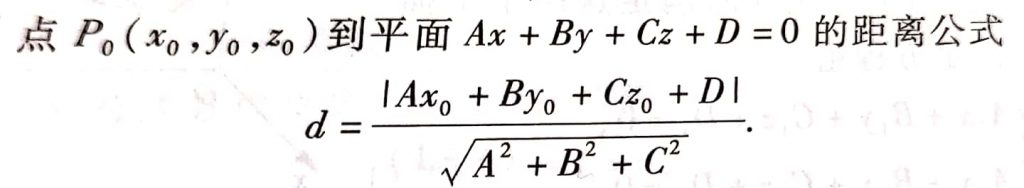

No responses yet